剩余价值定律

剩余价值定律

剩余价值定律

江苏无锡陆善民

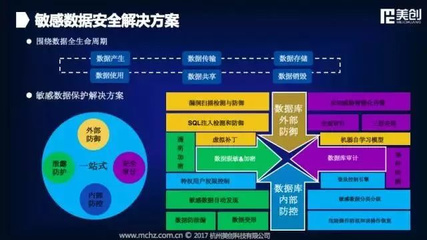
内容摘要：马克思所提出的剩余价值理论，亦即剩余价值定律，呈现多样化的表达方式剩余价值学说，既包括文字描述，亦涵盖数学公式的表述。其中，以数学公式呈现的剩余价值定律，其显著优势在于便于进行数学运算。本文列举了若干数学公式形式的剩余价值定律，旨在为后续对国际贸易比较优势及汇率的分析提供坚实的理论基础。

假设某公司专注于生产一种特定产品，为了制造该产品，公司总共投入了资本G，在这笔资本中，有一部分是不变资本Gc，另一部分则是可变资本Gv，从而形成了以下的关系：

公式（1）表达了G等于Gc与Gv之和。

若设定不变资本Gc的周转速度为Fc（以每年次数计），那么在一年时间里，不变资本所转移的价值，即生产资料的转移价值，可表示为Dc（Dc亦称作不变成本）：

Dc 等于 Gc 乘以Fc，即：Dc = Gc * Fc ——（2）

若设定可变资本Gv的周转速度为Fv（以每年次数计），那么在一年时间内，可变资本的周转次数所对应的总量，即劳动者年度的总工资，可表示为Dv（同时Dv也被称作可变成本）：

Dv 等于 Gv 乘以 Fv，即：Dv = Gv * Fv ——（3）

商品的总成本是由不变成本Dc和劳动者年工资Dv共同构成的，这个总和可以用符号D来表示。

等式D等于Gc乘以Fc加上Gv乘以Fv，即D等于Dc加上Dv……（4）

若以W代表全年商品的销售总收入，那么W与商品成本D之间的差额即为年度的剩余价值剩余价值定律，此剩余价值我们用M来表示。

M 等于 W 减去 D，即 M = W - D；进一步分解，M 等于 W 减去 Dc 再减去 Dv，表示为 M = W - Dc - Dv。----（5）

假设将剩余价值M拆分为企业所获利润L与国家所收税费S两大组成部分（在此情境中，我们暂未考虑诸如利息、地租等其他形式的剩余价值转换），据此可得：

M等于L加S，同时W等于Dc加Dv再加M，或者W等于Dc加Dv再加L再加S。

税收属于剩余价值的范畴，恩格斯曾引用马克思的论述来证明这一点：“马克思通过举例阐述了七十一先令的剩余价值总额所呈现的不同分配方式，包括什一税、地方税和国税共计二十一先令，地租二十八先令，农场主的利润和利息二十二先令，总计构成七十一先令的剩余价值。”（【1】）

公式（6）阐述了全年商品销售收入W的构成，它由不变成本Dc、劳动者年工资Dv、企业利润L以及税费S四部分组成。此公式与公式（5）共同构成了剩余价值定律的两种数学模型。

根据公式（4），我们定义垫付资本G的平均周转率F：

公式F等于D，而G等于（GcFv加上GvFv）除以G，即——（7）

公式（7）揭示了垫付资本G的周转速度F，这一速度是固定资本Gc的周转速度Fc与变动资本Gv的周转速度Fv按照一定权重计算得出的平均值。此外剩余价值学说，我们引入剩余价值率μ（单位：1/年）这一概念，该率是全年创造的剩余价值M与垫付资本G之间的比率。

μ等于M除以G，也就是L加S除以G，即L除以G加上S除以G，公式表示为――――――――――――――――（8）。

公式（8）中的L/G代表的是年度利润比率，而S/G则反映了全年税费收入与垫付资本G之间的税率关系，因此，公式（8）揭示了剩余价值比率等同于利润比率与税率之和。据此，我们可以从公式（6）推导出剩余价值定律的另一种表述形式：

W等于Dc加上Dv加上L加上S，即等于（F加上μ）乘以G，公式（9）如下所示。

参量F与μ的量纲为每一年，而（F＋μ）的倒数则对应时间的量纲，即年，我们用符号T来表示这一量纲，并将其命名为企业的生产时间常数。

时间T等于F加μ的倒数，即T＝1/（F＋μ），这等于G除以W，即T＝G/W。----(10)

现在，垫付资本G和销售收入W之间的关系可以用下式表示：

G 等于 T 乘以 W……（11）

若所涉企业年度产出达到Q量，且商品售价设定为p，那么总销售额W可表示为Q乘以p，将此等式代入公式(11)剩余价值定律，即可导出剩余价值定律的另一种表述方式。

公式G等于时间乘以质量再除以能量，即G等于TpQ。——（12）

公式（12）阐述了垫付资本G、企业生产时间常数T、商品单价p以及年产量Q之间的相互关系。该公式的推导过程颇为曲折，其目的在于强调企业的生产时间常数与垫付资本的周转速度、盈利水平、税率等因素密切相关。在后续讨论中剩余价值学说，我们将借助公式（12）来探讨国际贸易的比较优势以及汇率问题。

通过对2002年众多上市公司资料的汇总分析，我发现不同领域的生产时间常数T存在显著差异。具体来看，以下行业的时间常数表现尤为突出：房地产行业的时间常数T为3.52；水电气行业的时间常数T为4.01；交通仓储行业的时间常数T为3.23；采掘业的时间常数T为1.15；电子行业的时间常数T为1.45；医学生物行业的时间常数T为1.50。

这些参数可供讨论国际贸易时参考。

（lu_shan_min@163）

参考书目

【1】恩格斯：《反杜林论》，人民出版社出版，第209页。